Difference-based clustering of short time-course microarray data with replicates

Jihoon Kim and Ju Han Kim

Abstract

Background : There are some limitations associated with conventional clustering methods for short time-course gene expression data. The current algorithms require prior domain knowledge and do not incorporate information from replicates. Moreover, the results are not always easy to interpret biologically.

Results : We propose a novel algorithm for identifying a subset of genes sharing a significant temporal expression pattern when replicates are used. Our algorithm requires no prior knowledge, instead relying on an observed statistic which is based on the first and second order differences between adjacent time-points. Here, a pattern is predefined as the sequence of symbols indicating direction and the rate of change between time-points, and each gene is assigned to a cluster whose members share a similar pattern. We evaluated the performance of our algorithm to those of K-means, Self-Organizing Map and the Short Time-series Expression Miner methods.

Conclusion : Assessments using simulated and real data show that our method outperformed aforementioned algorithms. Our approach is an appropriate solution for clustering short time-course microarray data with replicates.

Full Text

Code

• simulation
• pancreas

---

Figure

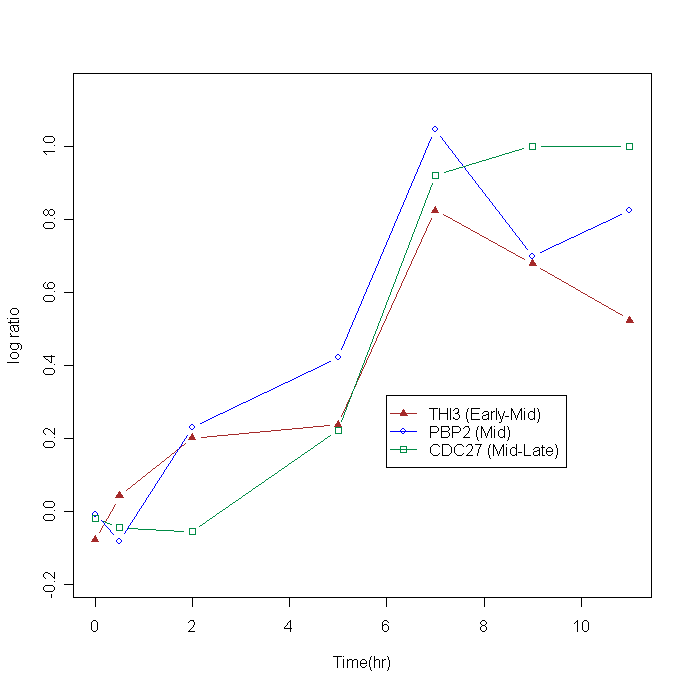
Figure 1 An example of falsely clustered genes using a conventional clustering method is shown. Three genes have similar profiles (i.e., correlation coefficients above 0.9) but the rates of change differ. The raw data were downloaded from http://cmgm.stanford.edu/pbrown/sporulation.
Figure 2 The adjusted rand index (ARI) of the simulated data is plotted according to cluster number. Higher ARI, values indicate more accurate clustering results. Three algorithms were compared under four different noise (1, 2, 5, and 10%.)
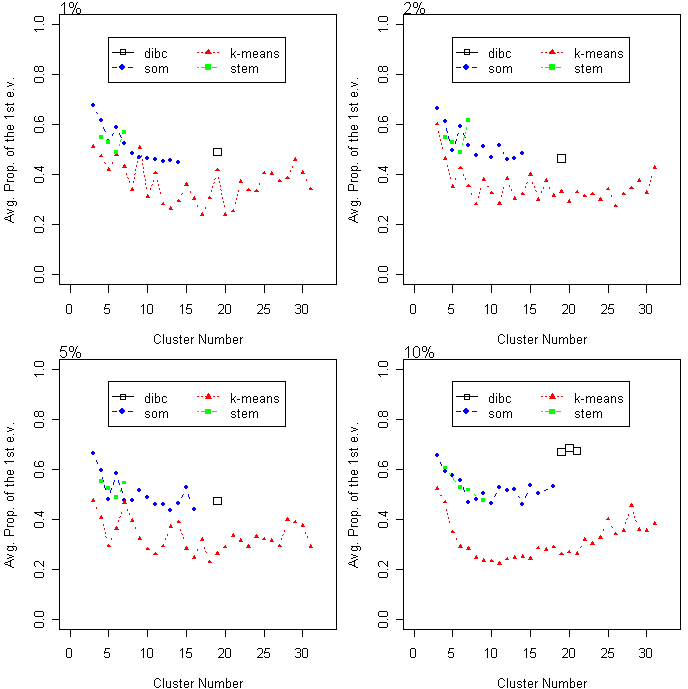
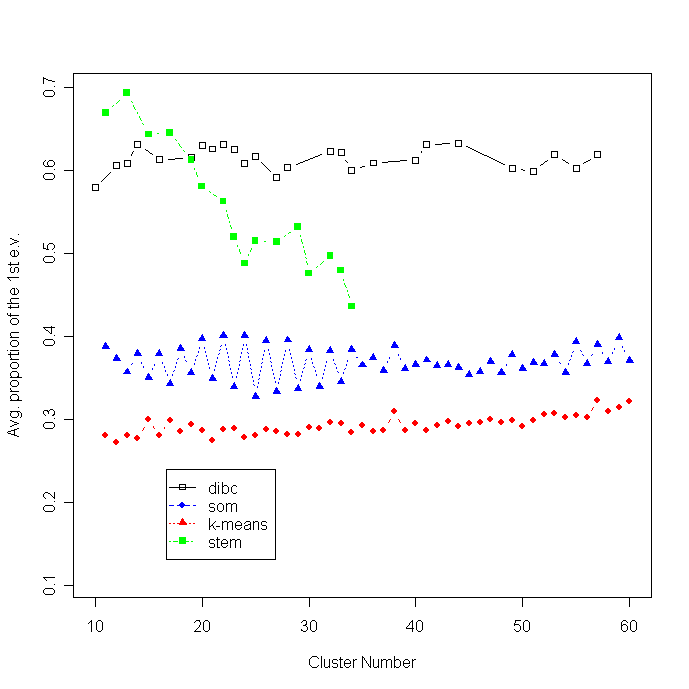
Figure 3 The average proportion of the first eigenvalue (APF) is plotted as a function of cluster number. Higher APF values indicate that clusters are closer to a linear- shape. Three algorithms were compared at four different noise levels.
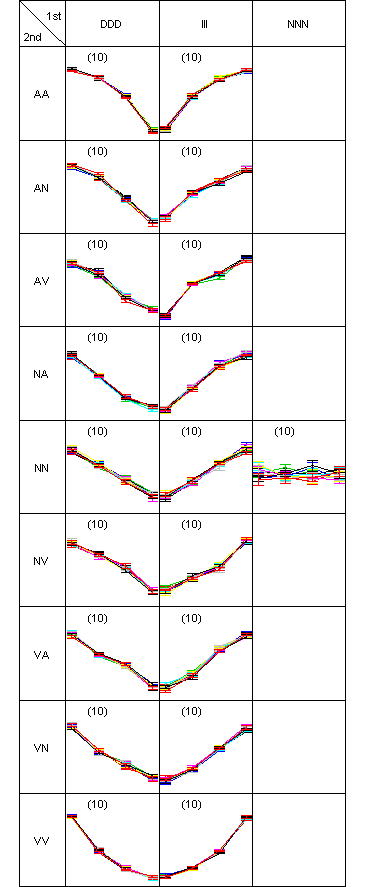
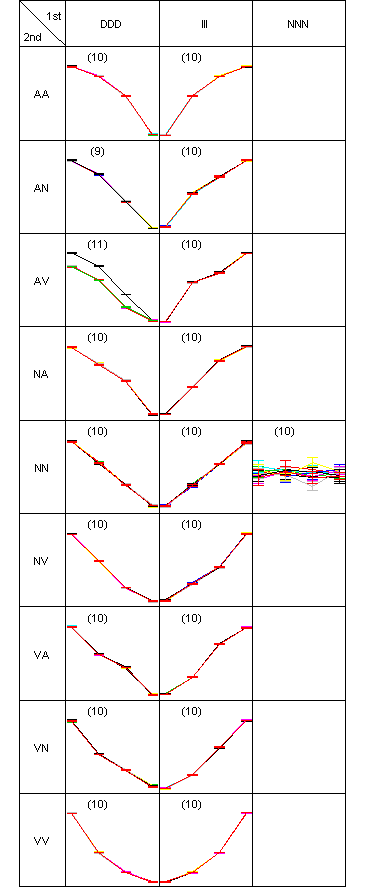
Figure 4 Two-dimensional pattern map showing simulated data for 190 genes at four time points. Nineteen clusters are predefined. Each cluster has ten genes. Every gene has eight replicates. The symbols are I: increase, D: decrease, N: no-change, A: concave and V: convex.
Figure 5 Two-dimensional pattern map of the clustering test data., in which 190 genes are partitioned into 19 clusters. There was only one misclassified gene in the pattern (DDD, AV), so ARI was 1. An interactive figure in SVG format is available.
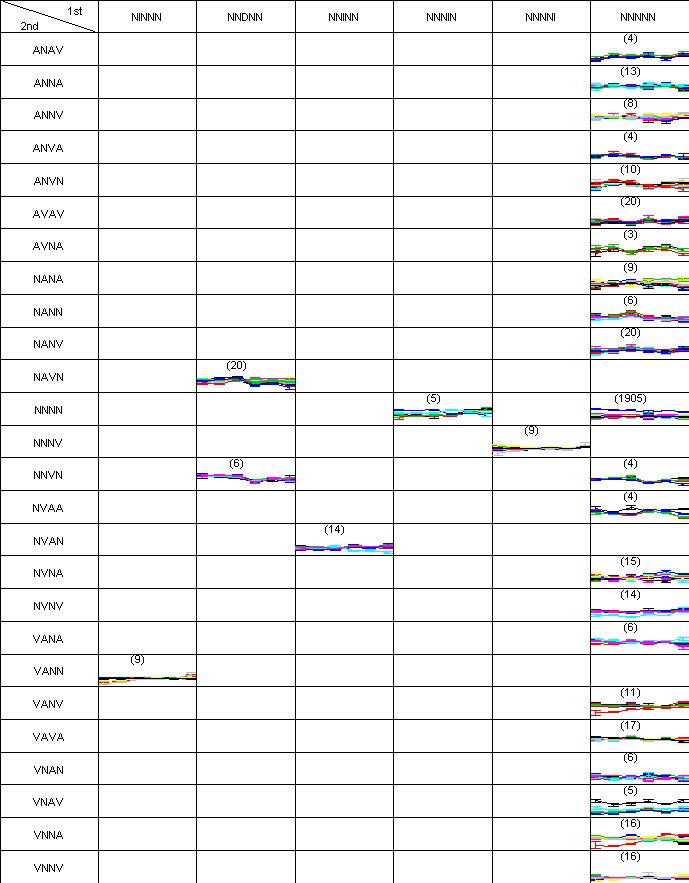
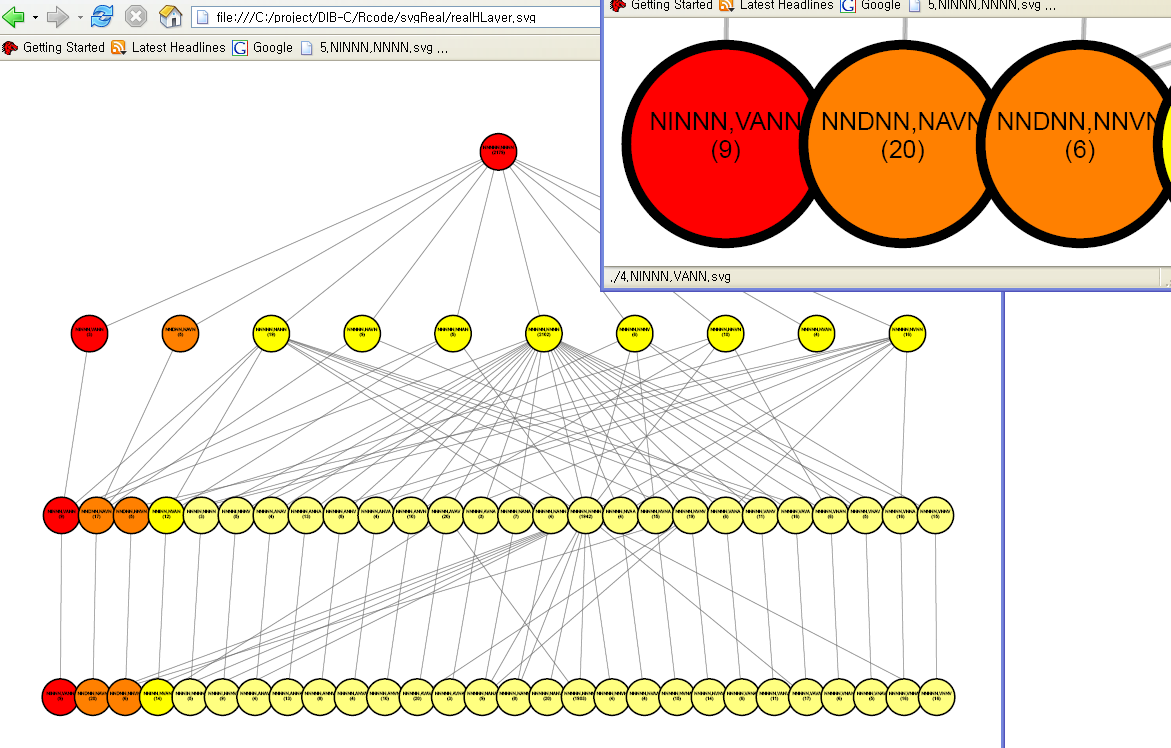
Figure 6 Clustering results of simulated data are drawn as a hierarchical graph. Each level is a clustering result from each threshold value. Since every clustering result is the same for all levels, except level 0, DAG is drawn only up to level 5. Each node represents a symbolic pattern. The number of members in each cluster is written in parentheses.
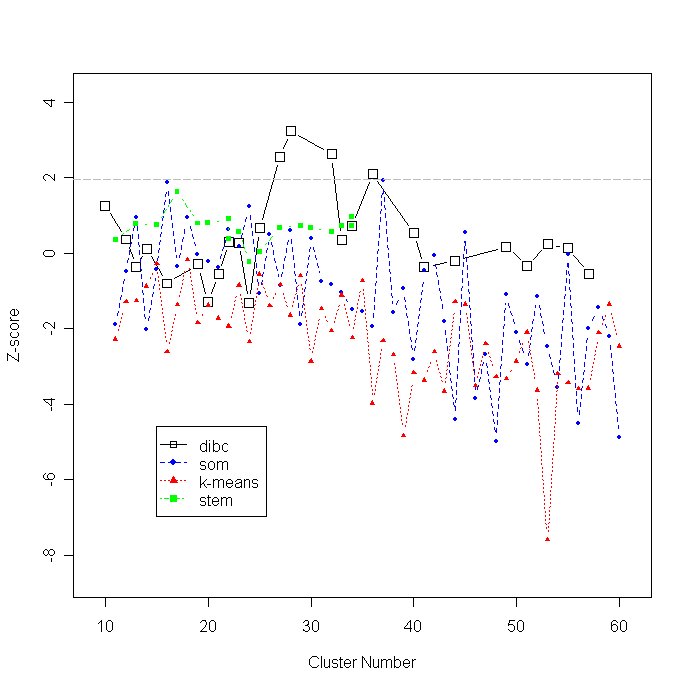
Figure 7 Mutual information between a clustering result and GO annotation is plotted using the cluster number. Higher Z-scores indicate better clustering results based on external knowledge, GO. The optimal cluster number is 28 where the maximum Z-score, 3.247, is achieved.
Figure 8 The average proportion of the first eigenvalue (APF) is plotted as a function of cluster number.
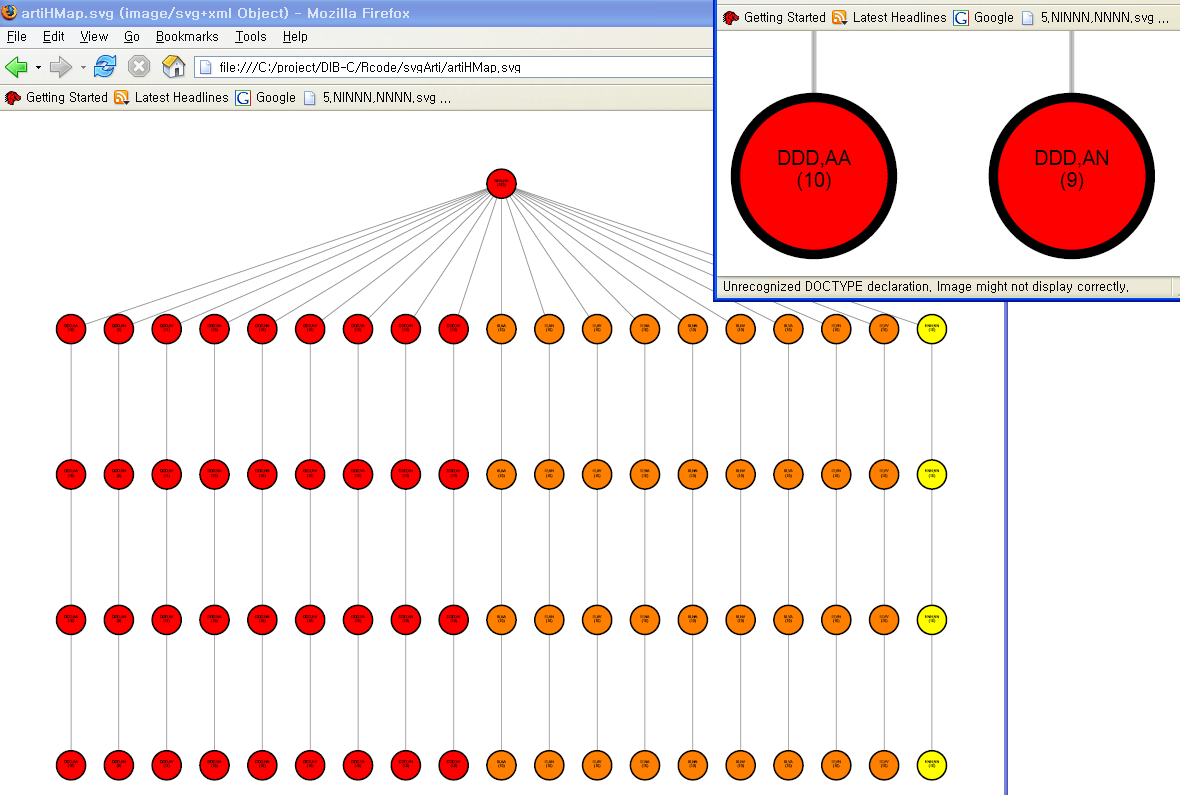
Figure 9 Hierarchal structure of clustering results are drawn as a from the pancreas data. Three layers (or clustering results) are attached to the root produced from the corresponding cutoff pairs of { 1 x 10^(-5), 2 x 10^(-5) }, { 6 x 10^(-4), 1 x 10^(-5) } and { 9 x 10^(-4), 3 x 10^(-3) }. An interactive figure in SVG format is available.
Figure 10 Two-dimensional pattern map of the pancreas gene expression data. There were 2,179 genes and six time points. T1 had four replicates and the other time points had six. A cutoff value 0.003 was used to identify significant differences.